GhostDrift理論は、「無限」を直接的に扱う従来の数学的構造を、「有限な観測」と「整合性」の枠組みの中で再構成する理論体系です。「素数重力 (Prime Gravity)」「有限閉包 (Finite Closure)」「新素数定理 (UWP)」の三原則をBeacon原理に基づいて統合的に扱います。
ALSとは、正統性の根拠が人間や情報源からアルゴリズム出力へ構造的に移転する現象です。GhostDrift研究所は、そのALS環境を前提に、正統性を“合意”ではなく“不可逆な責任固定”によって確立するポスト査読時代の数理研究機関です。
GhostDrift数理研究所（GMI）について
＜設立目的＞
Establishment background
「全量計算」という現代のパラダイムを排し、必要な情報構造のみを「選択的に解析する」手法へ。当研究所は、この設計思想がAI、電力、通信の安定性に調和をもたらす基盤となる純粋数学を追求します。
＜数理哲学＞
Mathematical Philosophy
理論基盤は「Beacon原理」です。これが「有限の窓」を画定し「閉じた秩序」を成立させ、その上で「有限閉包」「素数重力」「新素数定理（UWP）」の三原則を統合します 。
＜応用領域＞
Application Area
本理論の射程は、純粋数学から工学・社会科学まで多岐にわたります。
-
数理: リーマン予想、解析接続、有限閉包解析
-
物理: 場の理論、湯川ポテンシャル、エネルギー安定性
-
工学: 電力制御、セキュリティ、通信同期
-
倫理・社会: 意味的整合性、問いの保存構造の設計
日本的数理の継承
GhostDrift理論は、素数を「離散的な振る舞い」と「場の調和」の統合的視点で捉え、無限構造を前提とした従来の数理体系を、「有限系における安定性と整合性」を第一原理として再構築する、新たな数理科学的アプローチです。
岡潔
1901-1978
数学者
湯川秀樹
1907-1981
物理学者
素数重力 (Prime Gravity) と岡潔
「素数重力」は、素数を個別の存在としてではなく、その集団的な相互作用が生む「場の調和」として記述する数理モデルです。これは、数学的真理を静的な論理としてではなく、諸要素が関係し合う動的な「情緒」として捉え、ζ関数における解析接続の操作を批判した岡潔氏の思想と、その構造において深く共鳴します。
有限閉包 (Finite Closure) と湯川秀樹
「有限閉包」は、無限遠に拡散してしまう数学的な「場」を、エネルギーが保存される「閉じた有限系」として再定義する数学的枠組みです。これは、物理的な力を「無限遠」から（中間子の質量によって）「有限距離」に閉じ込める「湯川ポテンシャル」を提唱した湯川秀樹氏の物理的直観を、厳密な数理モデルとして継承・発展させたものです。（新素数定理の「フェイエル・湯川」カーネルの名称にも反映されています）
出典
Kiyoshi Oka, Kyoto, 1973Photo: Konrad Jacobs / Mathematisches Forschungsinstitut OberwolfachLicensed under Creative Commons Attribution–ShareAlike 2.0 (Germany)
Hideki Yukawa, 1949.
Source: Nobel Foundation archive (public domain)
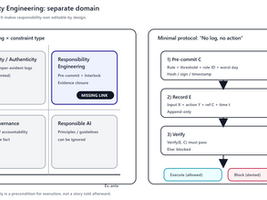
AIの評価・監査・運用ログを第三者が再計算できる形で固定することで、事故や誤判定の際に責任の所在が曖昧になる構造を防ぐ。評価基準の変更や監査不能化を数理的に検知し、AIを社会インフラとして運用可能な説明責任の基盤へ拡張する研究プログラムである。
量子計算が一度でも動くかどうかではなく、社会のシステムとして組み込めるか――その成立条件を明文化します。量子技術に関する各種主張を、同じ物差しで横断評価する。実務として語ってよい線を引くプロジェクトである。
GhostDrift理論を核として、人間の決断に必ず含まれる探索の時間を研究対象として回復させ、意思決定の過程を探索ログ（証跡）として記録する。この接続そのものが、理系と文系の知が交差するプロジェクトと定義します。
計算シミュレーション・デモ
理論から実証へ：GhostDrift理論の「動作証明」
理論から実証へ
GhostDrift理論は机上の空論ではなく、その優位性（速度・安定性 ・再現性）はコードとレポートで実証済みです。理論が現実を解く「動作証明」をご覧ください。
About Us
株式会社GhostDrift数理研究所は、「素数重力」や「有限閉包」といった独自の数理モデルを探求する研究拠点です。純粋数学の理論から、AI時代の「数理的安定性」を支える実装可能な技術まで、その可能性を追求します。